Gradient Index Lenses

Scott Prahl

Sept 2023

[1]:

%config InlineBackend.figure_format='retina'

import sys
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.patches as patches

if sys.platform == "emscripten":
    import piplite

    await piplite.install("pygrin")

import pygrin

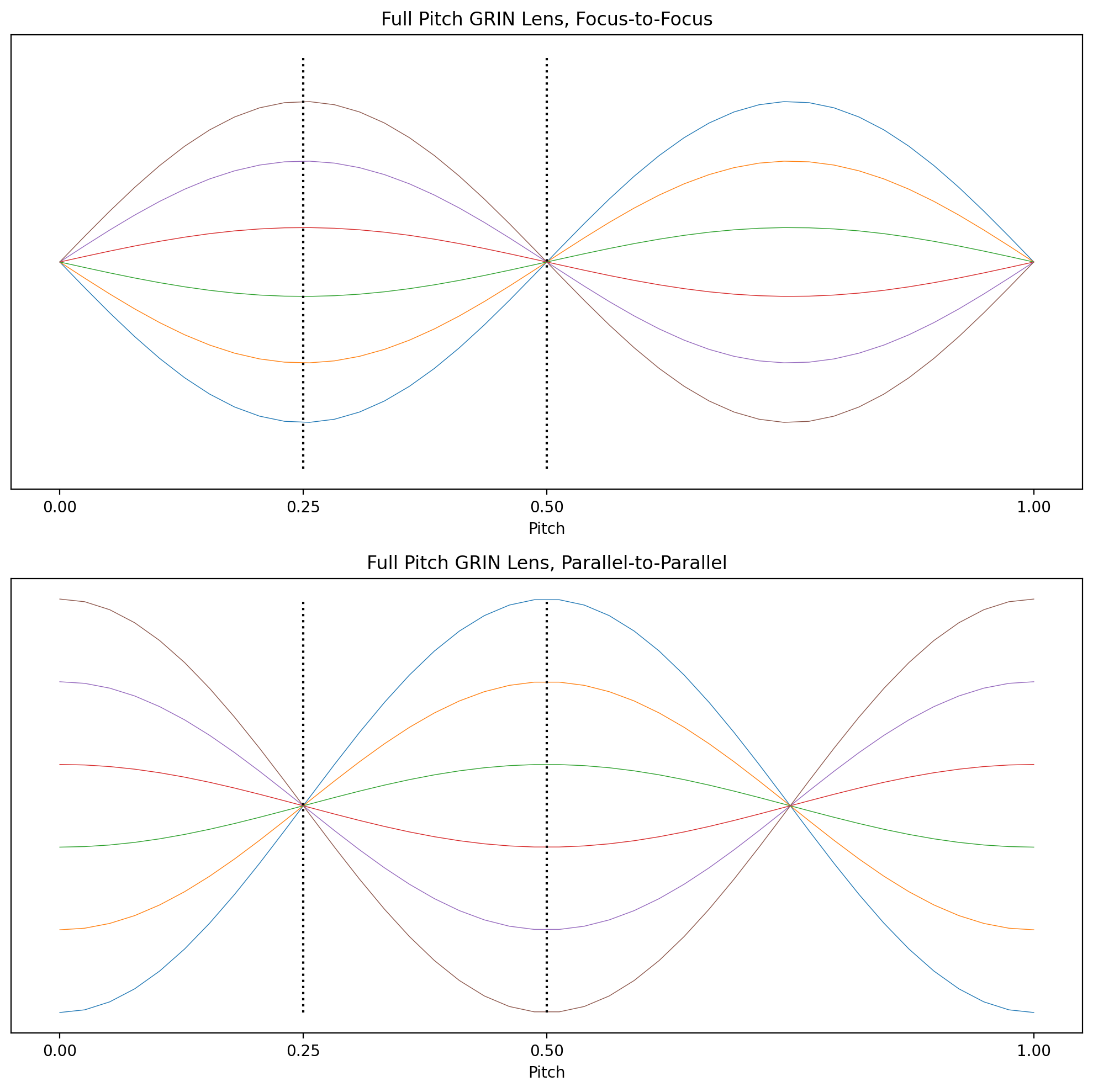
Pitch of a GRIN lens

A gradient index (GRIN) lens is characterized by a sinusoidal ray path along the lens. A lens is typically characterized by its pitch or the number of sinusoidal periods within the lens.

If the pitch is one (or an integer) then the grin lens acts as a relay and reproduces the light incident on the entrance surface at the exit surface. A half-pitch inverts the pattern. A quarter-pitch lens will collimate a point source or focus a collimated incident beam.

[2]:

n0 = 1.608  # centerline index of refraction
length = 1  # mm
diameter = 0.25  # mm
angle = 40 * np.pi / 180  # radians
xpos = 0
pitch = 1
radius = diameter / 2

# max angle in air
max_angle = pygrin.max_angle(n0, pitch, length, diameter)
# range of launch angles
angles = np.linspace(-max_angle, max_angle, 6)
# range of launch angles in grin lens
angles = np.arcsin(np.sin(angles / n0))

plt.subplots(2, 1, figsize=(10, 10))
plt.subplot(2, 1, 1)
for angle in angles:
    z, r = pygrin.meridional_curve(n0, pitch, length, xpos, angle)
    plt.plot(z, r, lw=0.5)

plt.plot([0.25 * length, 0.25 * length], [-radius, radius], ":k")
plt.plot([0.5 * length, 0.5 * length], [-radius, radius], ":k")

plt.xticks([0, 0.25, 0.5, 1.0])
plt.yticks([])
plt.xlabel("Pitch")
plt.title("Full Pitch GRIN Lens, Focus-to-Focus")

plt.subplot(2, 1, 2)
for xpos in np.linspace(-radius, radius, 6):
    z, r = pygrin.meridional_curve(n0, pitch, length, xpos, 0)
    plt.plot(z, r, lw=0.5)

plt.plot([0.25 * length, 0.25 * length], [-radius, radius], ":k")
plt.plot([0.5 * length, 0.5 * length], [-radius, radius], ":k")

plt.xticks([0, 0.25, 0.5, 1.0])
plt.yticks([])
plt.xlabel("Pitch")
plt.title("Full Pitch GRIN Lens, Parallel-to-Parallel")
plt.tight_layout()  # Ensures proper spacing

# plt.savefig('pitch.png', dpi=300)
plt.show()

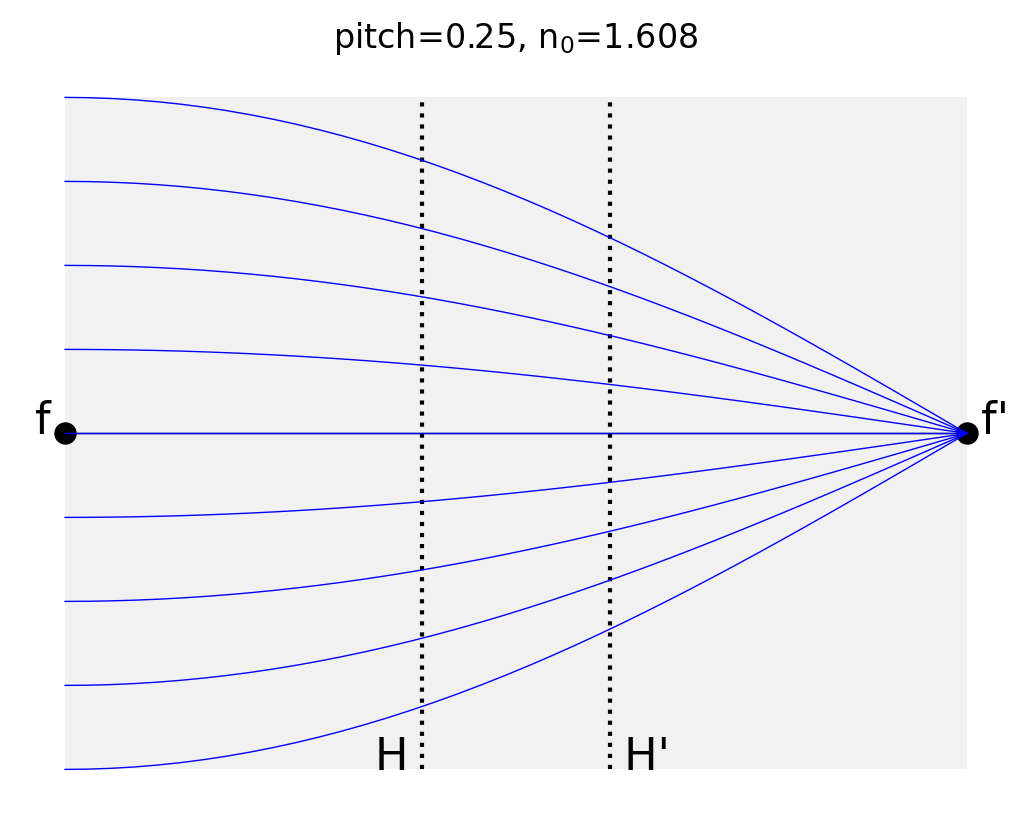
Quarter Pitch

This is the typical example because collimated light is focused to a point, or conversely, a point source is collimated. Here we see an example the former.

[3]:

pitch = 0.25
n0 = 1.608  # centerline index of refraction
length = 5  # mm
diameter = 2  # mm
angle = 0 * np.pi / 180  # radians

pygrin.plot_principal_planes(n0, pitch, length, diameter)
xpos = np.linspace(-diameter / 2, diameter / 2, 9)
for pos in xpos:
    z, r = pygrin.meridional_curve(n0, pitch, length, pos, angle)
    plt.plot(z, r, color="blue", lw=0.5)

plt.rcParams["figure.figsize"] = [10, 3]
plt.axis("off")
plt.show()

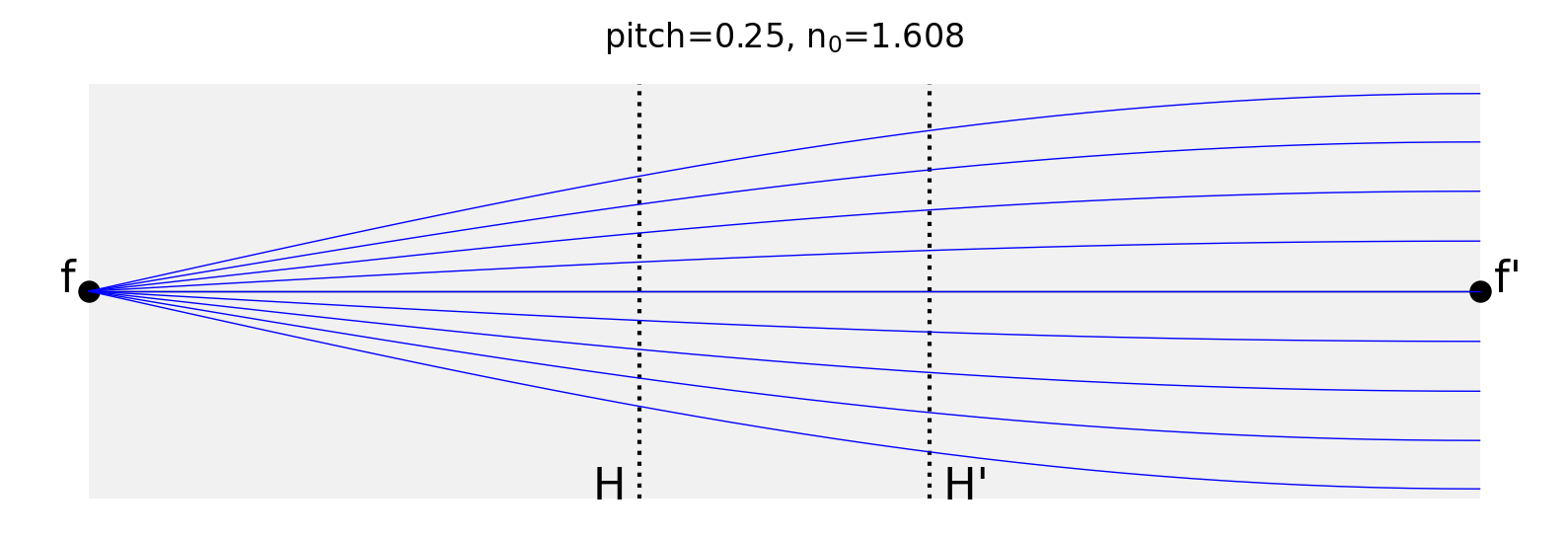
This shows light being collimated from a point source

[4]:

pitch = 0.25
n0 = 1.608  # centerline index of refraction
length = 5  # mm
diameter = 2  # mm
xpos = 0  # mm

pygrin.plot_principal_planes(n0, pitch, length, diameter)

# max angle in air
max_angle = pygrin.max_angle(n0, pitch, length, diameter)
# range of launch angles
angles = np.linspace(-max_angle, max_angle, 9)
# range of launch angles in grin lens
angles = np.arcsin(np.sin(angles / n0))

for angle in angles:
    z, r = pygrin.meridional_curve(n0, pitch, length, xpos, angle)
    plt.plot(z, r, color="blue", lw=0.5)

plt.rcParams["figure.figsize"] = [10, 3]
plt.axis("off")
plt.show()

Here is a 4f system. Here the source on the left is on focal distance from the front face and the

[5]:

# 4f system
pitch = 0.25
n0 = 1.608  # centerline index of refraction
length = 5  # mm
diameter = 2  # mm
zobj = pygrin.EFL(n0, pitch, length)
xpos = np.linspace(-diameter / 4, diameter / 4, 9)

pygrin.plot_principal_planes(n0, pitch, length, diameter)

for pos in xpos:
    z, r = pygrin.full_meridional_curve(n0, pitch, length, -zobj, 0.0, pos)
    plt.plot(z, r, color="blue", lw=0.5)

plt.rcParams["figure.figsize"] = [10, 3]
plt.axis("off")
plt.show()

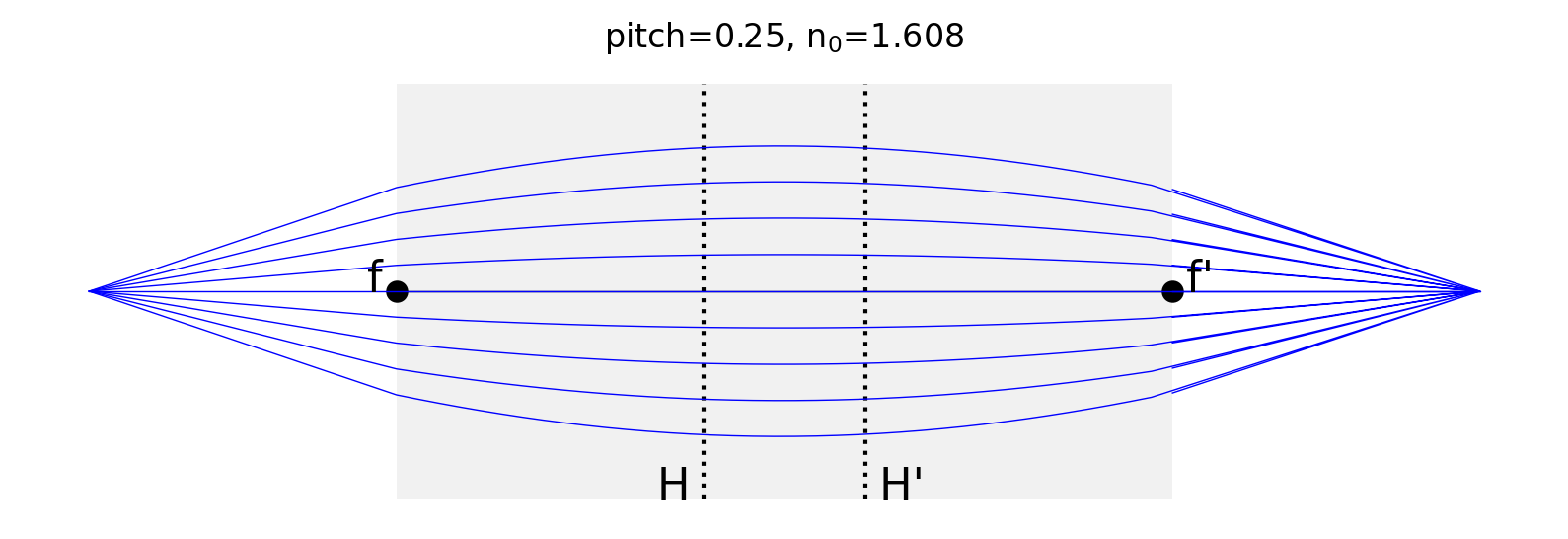
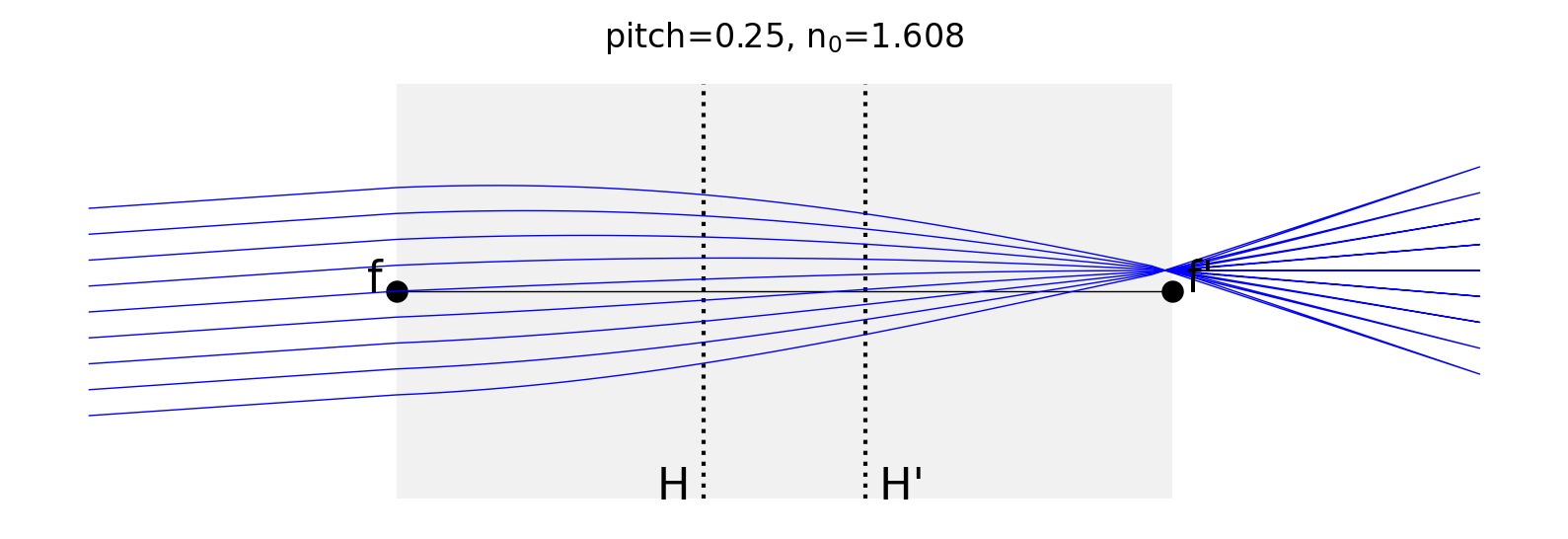
Finally, this shows that collimated light incident at an angle on the lens will be imaged to a point off-axis.

[6]:

# off axis launch
pitch = 0.25
n0 = 1.608  # centerline index of refraction
length = 5  # mm
diameter = 2  # mm
zobj = pygrin.EFL(n0, pitch, length)
xpos = np.linspace(-diameter / 4, diameter / 4, 9)

pygrin.plot_principal_planes(n0, pitch, length, diameter)

for pos in xpos:
    z, r = pygrin.full_meridional_curve(n0, pitch, length, -zobj, pos - 0.1, pos)
    plt.plot(z, r, color="blue", lw=0.5)

plt.rcParams["figure.figsize"] = [10, 3]
plt.axis("off")
plt.show()

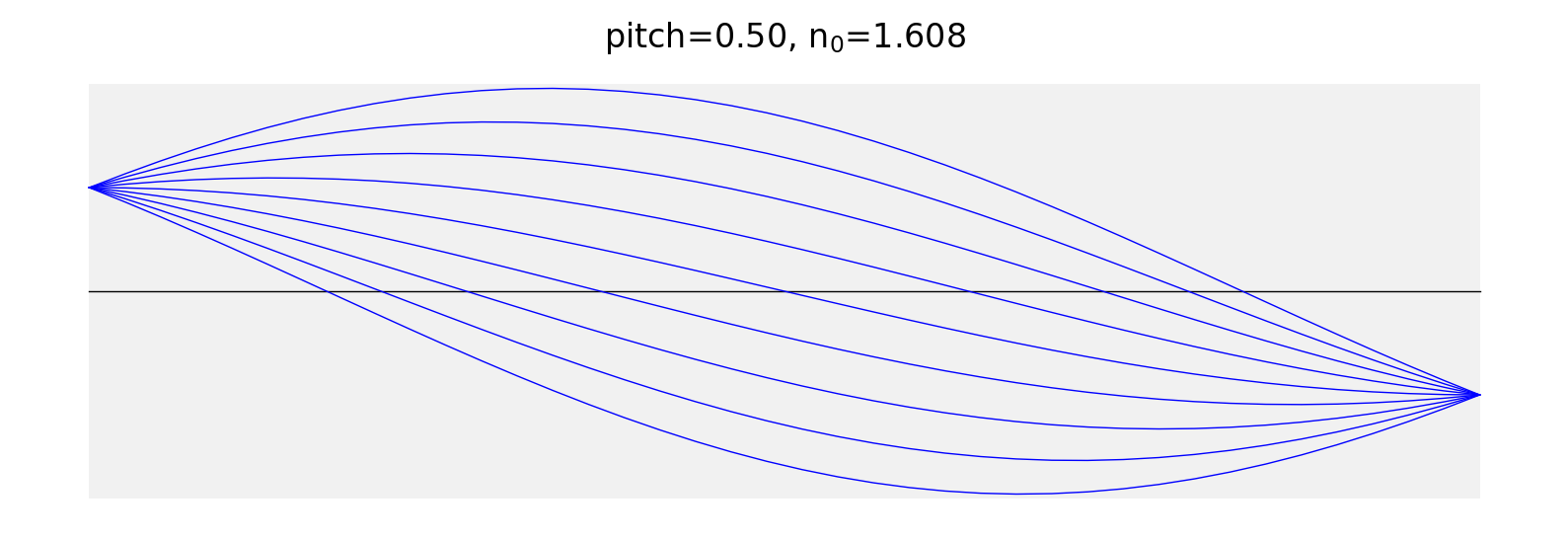
Half Pitch

Here we show that all the rays hitting the front surface at a point are imaged to the same point on the exit surface — but inverted.

The prinicipal planes are not drawn because the effective focal length is infinite.

[7]:

pitch = 0.5
n0 = 1.608  # centerline index of refraction
length = 5  # mm
diameter = 2  # mm
xpos = 0.5  # mm

pygrin.plot_principal_planes(n0, pitch, length, diameter)

# max angle in air
max_angle = pygrin.max_angle(n0, pitch, length, diameter)
# range of launch angles
angles = np.linspace(-max_angle, max_angle, 9)
# range of launch angles in grin lens
angles = np.arcsin(np.sin(angles / n0))

for angle in angles:
    z, r = pygrin.meridional_curve(n0, pitch, length, xpos, angle)
    plt.plot(z, r, color="blue", lw=0.5)

plt.rcParams["figure.figsize"] = [10, 3]
plt.axis("off")
plt.show()

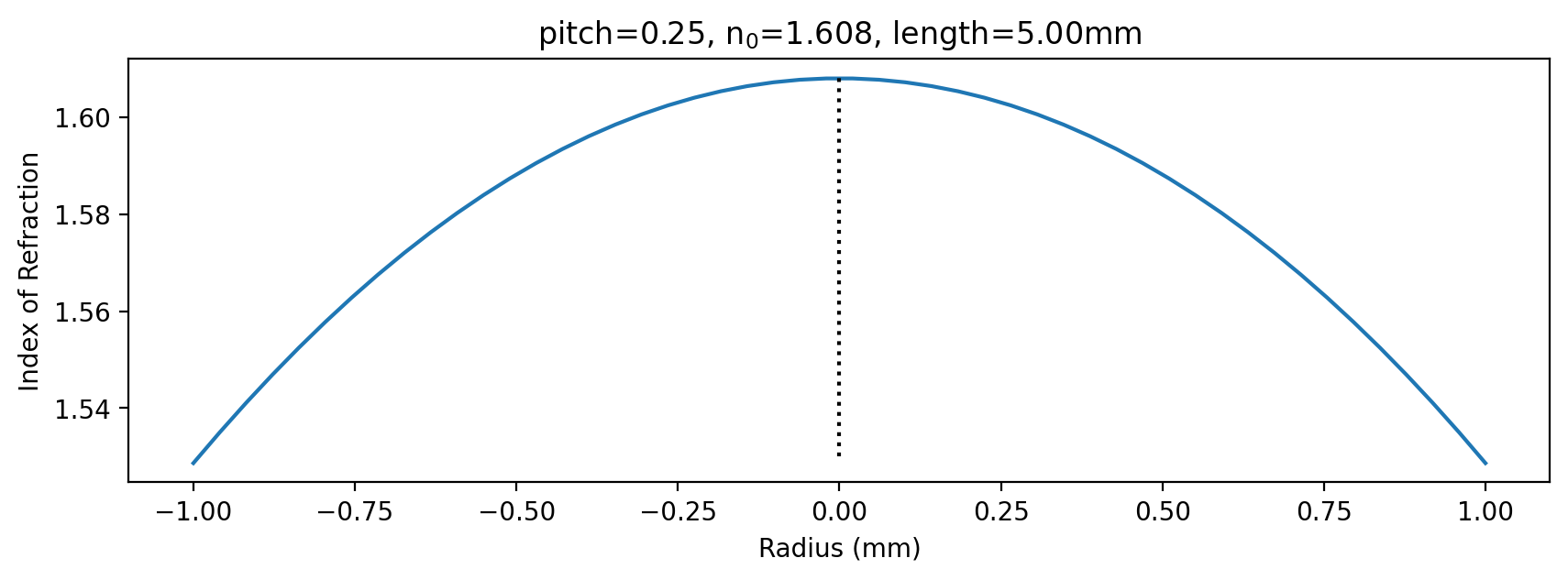
Index of Refraction Across Lens

Parabolic Profile

[8]:

n0 = 1.608
pitch = 0.25
length = 5  # mm
diameter = 2
r = np.linspace(-diameter / 2, diameter / 2, 50)

plt.plot(r, pygrin.parabolic_profile_index(n0, pitch, length, r))
plt.plot([0, 0], [1.53, n0], ":k")
plt.xlabel("Radius (mm)")
plt.ylabel("Index of Refraction")
plt.title(r"pitch=%.2f, n$_0$=%.3f, length=%.2fmm" % (pitch, n0, length))
plt.rcParams["figure.figsize"] = [6, 4]

plt.show()

Hyperbolic Secant Profile

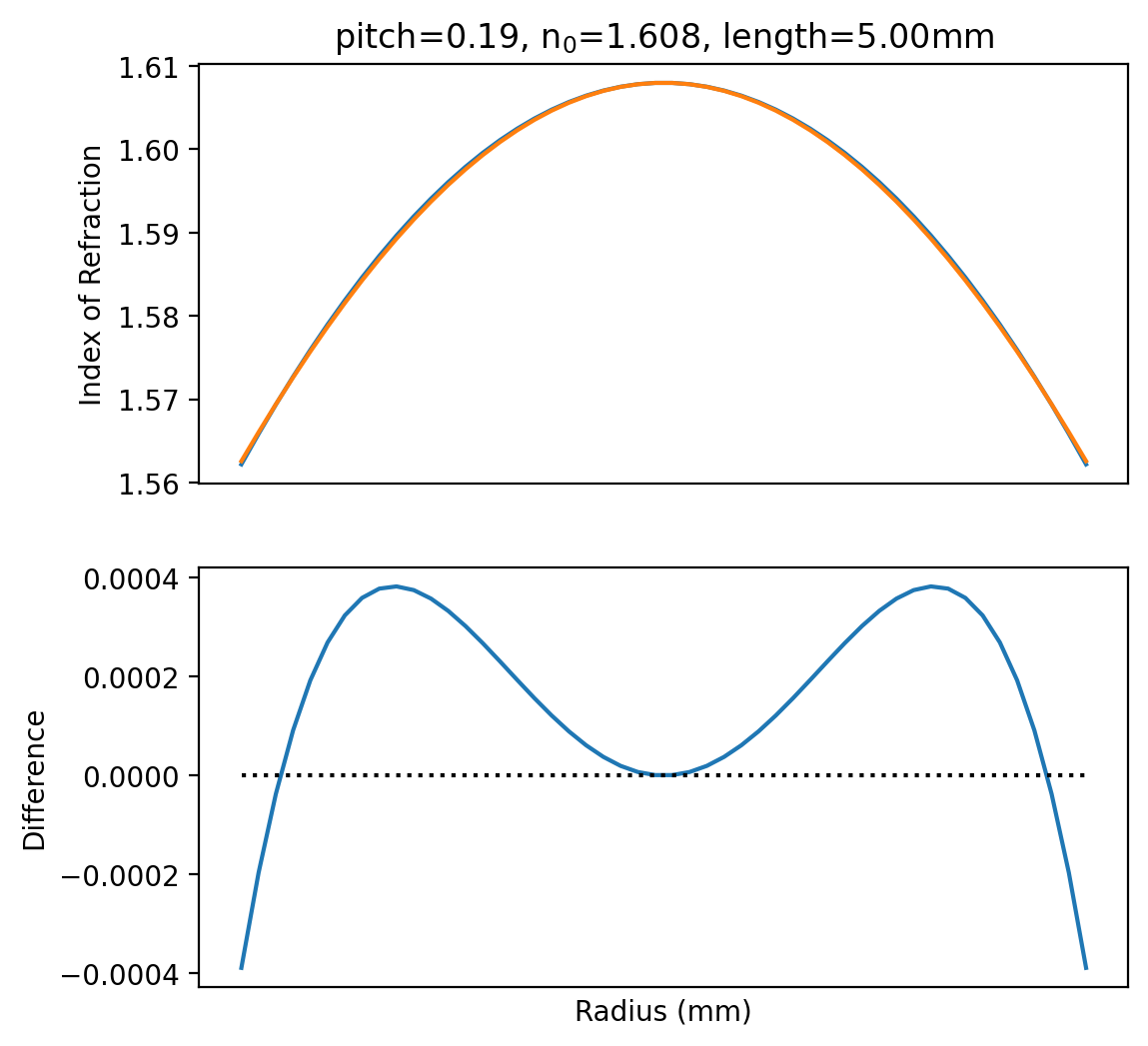
This has a few advantages over the parabolic profile: the propagation for a HS grin lens can be solved exactly and there aren’t any aberrations for meridional rays.

As you can see below, the HS profile can be quite close to the parabolic profile.

[9]:

n0 = 1.608
pitch = 0.19
length = 5  # mm
diameter = 2
gradient = pygrin.gradient(pitch, length)
alpha = 1.303 * gradient

r = np.linspace(-diameter / 2, diameter / 2, 50)

plt.subplots(2, 1, sharex=True, figsize=(6, 6))
plt.subplot(2, 1, 1)
n_p = pygrin.parabolic_profile_index(n0, pitch, length, r)
n_s = pygrin.hyperbolic_secant_profile_index(n0, alpha, r)
plt.plot(r, n_p)
plt.plot(r, n_s)
plt.xticks([])
plt.ylabel("Index of Refraction")
plt.title(r"pitch=%.2f, n$_0$=%.3f, length=%.2fmm" % (pitch, n0, length))
plt.rcParams["figure.figsize"] = [6, 4]

plt.subplot(2, 1, 2)
plt.plot(r, n_p - n_s)

plt.xlabel("Radius (mm)")
plt.ylabel("Difference")
plt.plot([-1, 1], [0, 0], ":k")

plt.show()

Catalog Examples

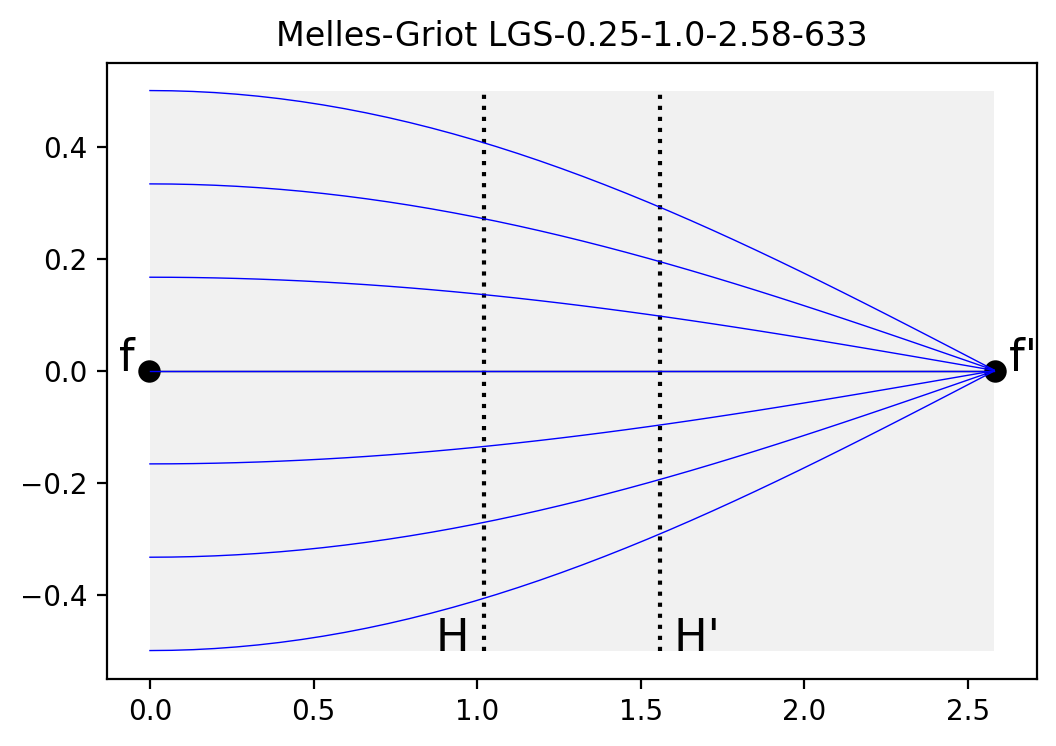
Grin Lens from ancient Melles Griot Catalog, 4.67 line 2

Part number LGS-0.25-1.0-2.58-633

[10]:

n = 1.608
gradient = 0.608
length = 2.58
diameter = 1

pitch = pygrin.period(gradient, length)
print("expected pitch = 0.25,           calculated %.2f" % pitch)

efl = pygrin.EFL(n, pitch, length)
na = pygrin.NA(n, pitch, length, diameter)
print("expected NA = 0.46,              calculated %.2f" % na)

angle = pygrin.max_angle(n, pitch, length, diameter)
print("expected full accept angle = 55°, calculated %.0f°" % (2 * angle * 180 / np.pi))

expected pitch = 0.25,           calculated 0.25
expected NA = 0.46,              calculated 0.46
expected full accept angle = 55°, calculated 54°

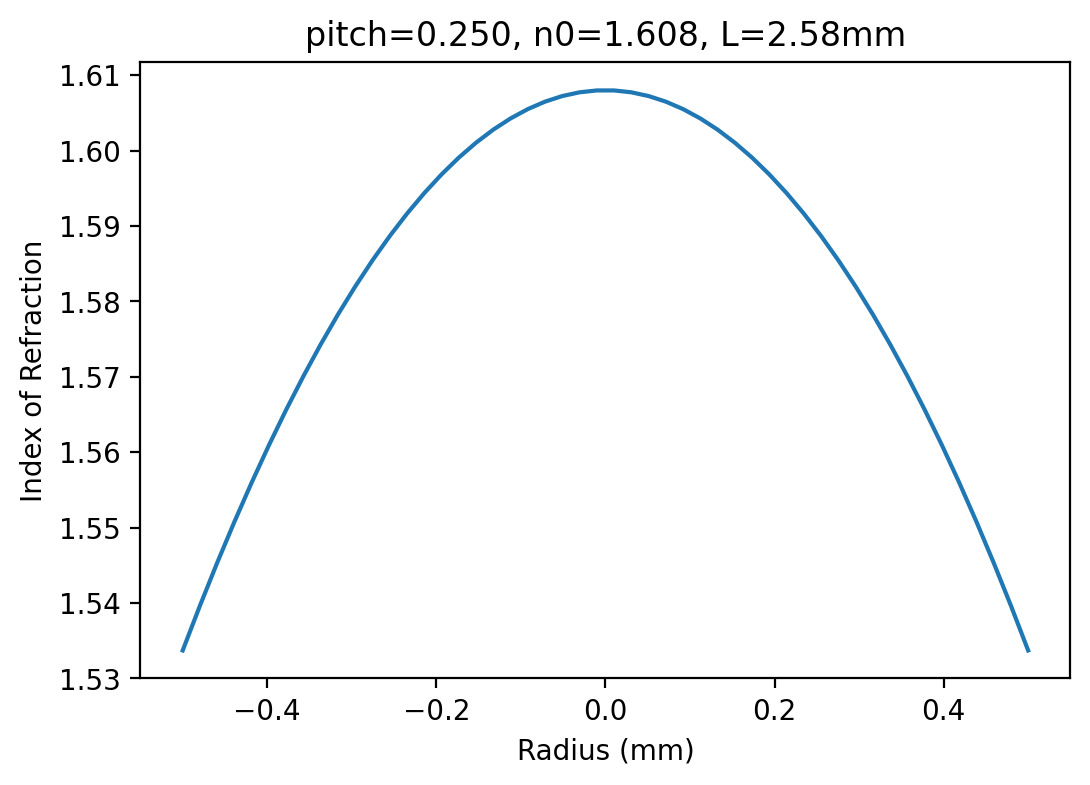
[11]:

r = np.linspace(-0.5, 0.5, 50)
plt.plot(r, pygrin.parabolic_profile_index(n, pitch, length, r))
plt.xlabel("Radius (mm)")
plt.ylabel("Index of Refraction")
plt.title("pitch=%.3f, n0=%.3f, L=%.2fmm" % (pitch, n, length))
plt.show()

[12]:

pygrin.plot_principal_planes(n, pitch, length, diameter)
xpos = np.linspace(-diameter / 2, diameter / 2, 7)
for pos in xpos:
    z, r = pygrin.meridional_curve(n, pitch, length, pos, 0 * np.pi / 180)
    plt.plot(z, r, color="blue", lw=0.5)

plt.title("Melles-Griot LGS-0.25-1.0-2.58-633")
plt.show()

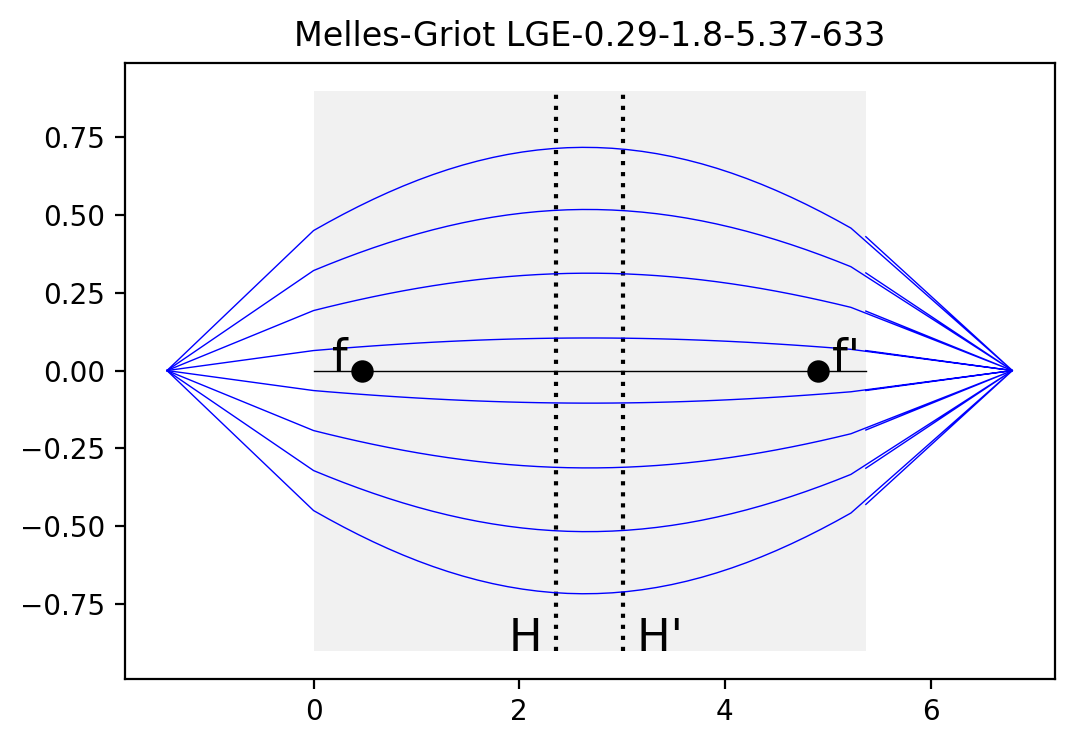
Grin Lens from ancient Melles Griot Catalog, 4.67 line 5

Part number LGE-0.29-1.8-5.37-633

[13]:

n = 1.608
gradient = 0.339
length = 5.37
diameter = 1.8

pitch = pygrin.period(gradient, length)
print("expected pitch = 0.29,            calculated %.2f" % pitch)

ffl = pygrin.FFL(n, pitch, length)
efl = pygrin.EFL(n, pitch, length)
print("expected FFL = 0.46,              calculated %.2f" % ffl)

na = pygrin.NA(n, pitch, length, diameter)
print("expected NA = 0.46,               calculated %.2f" % na)

angle = pygrin.max_angle(n, pitch, length, diameter)
print("expected full accept angle = 55°, calculated %.0f°" % (2 * angle * 180 / np.pi))

print("working distance = %.2f mm" % (efl - ffl))

expected pitch = 0.29,            calculated 0.29
expected FFL = 0.46,              calculated 0.47
expected NA = 0.46,               calculated 0.46
expected full accept angle = 55°, calculated 55°
working distance = 1.43 mm

[14]:

pygrin.plot_principal_planes(n, pitch, length, diameter)
xpos = np.linspace(-diameter / 4, diameter / 4, 8)
for pos in xpos:
    z, r = pygrin.full_meridional_curve(n, pitch, length, ffl - efl, 0, pos)
    plt.plot(z, r, color="blue", lw=0.5)

plt.title("Melles-Griot LGE-0.29-1.8-5.37-633")

plt.show()

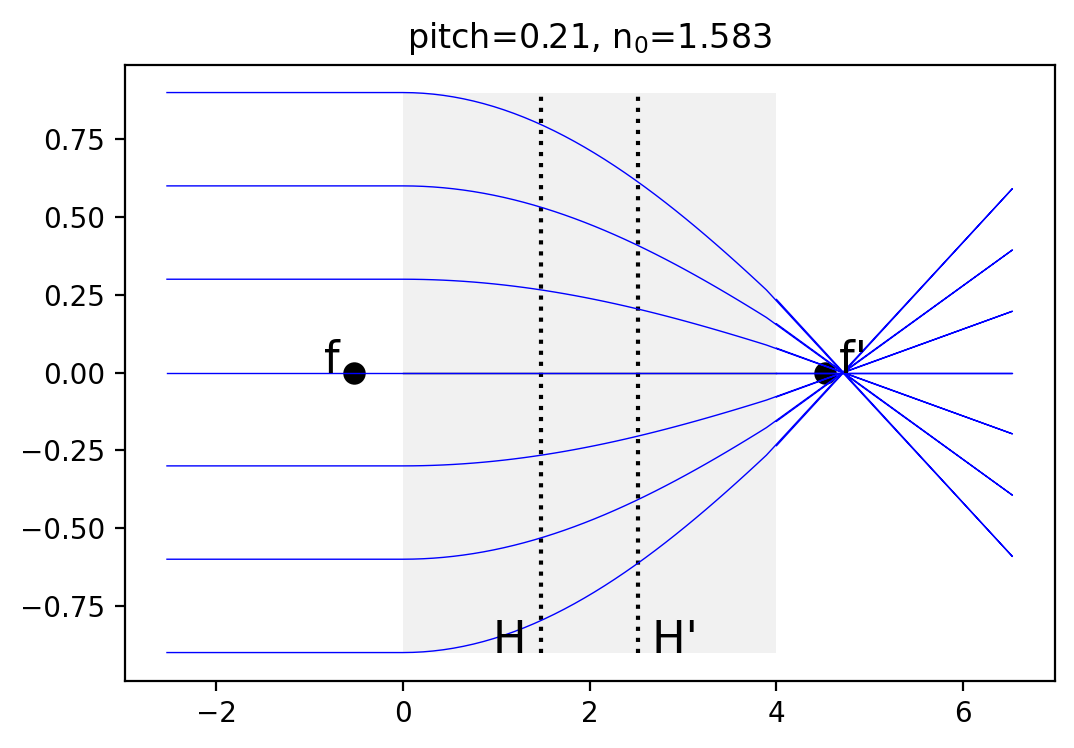
Riedl, page 96

[15]:

n = 1.5834
gradient = np.sqrt(0.1067)
length = 4
diameter = 1.8

pitch = pygrin.period(gradient, length)
print("expected pitch = 0.207,          calculated %.3f" % pitch)

efl = pygrin.EFL(n, pitch, length)
print("expected EFL = 2.00,             calculated %.2f" % efl)

ffl = pygrin.FFL(n, pitch, length)
print("expected FFL = -0.52,            calculated %.2f" % ffl)

bfl = pygrin.BFL(n, pitch, length)
print("expected BFL = 4.52,             calculated %.2f" % bfl)

na = pygrin.NA(n, pitch, length, diameter)
print("expected NA = 0.46,              calculated %.2f" % na)

angle = pygrin.max_angle(n, pitch, length, diameter)
print("expected full accept angle = 55°, calculated %.0f°" % (2 * angle * 180 / np.pi))

print("working distance = %.2f mm" % (-ffl + efl))

expected pitch = 0.207,          calculated 0.208
expected EFL = 2.00,             calculated 2.00
expected FFL = -0.52,            calculated -0.52
expected BFL = 4.52,             calculated 4.52
expected NA = 0.46,              calculated 0.44
expected full accept angle = 55°, calculated 52°
working distance = 2.53 mm

[16]:

pygrin.plot_principal_planes(n, pitch, length, diameter)
xpos = np.linspace(-diameter / 2, diameter / 2, 7)
for pos in xpos:
    z, r = pygrin.full_meridional_curve(n, pitch, length, ffl - efl, pos, pos)
    plt.plot(z, r, color="blue", lw=0.5)

plt.show()

Grin Lenses at Oregon Tech

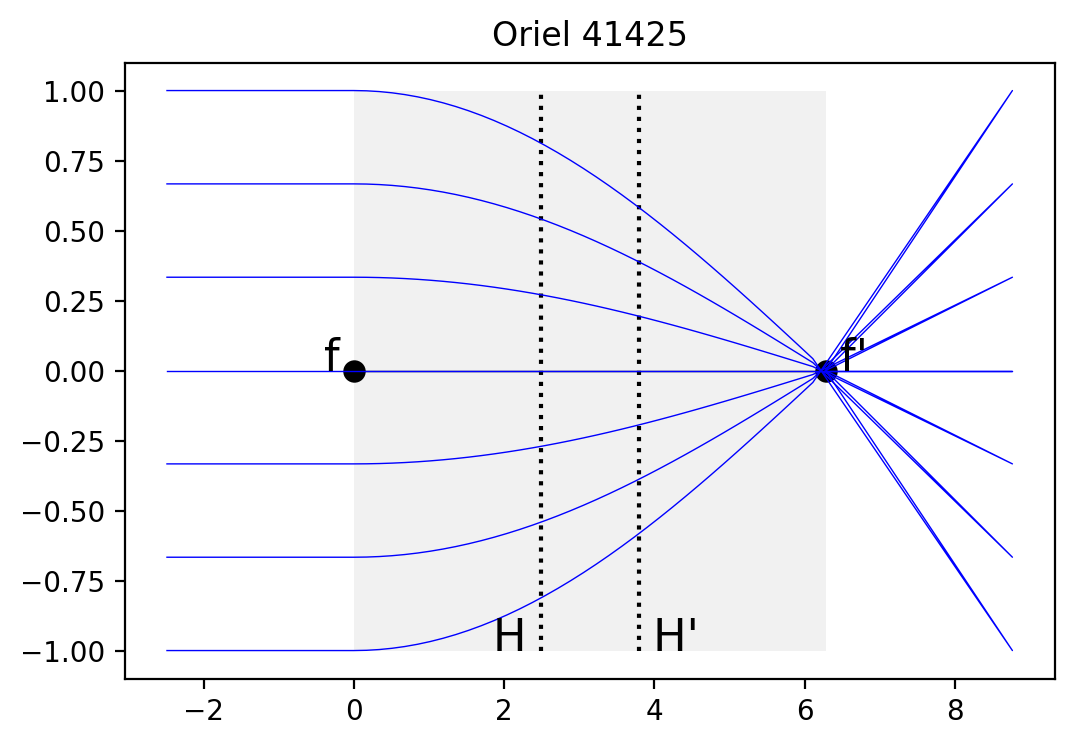
Oriel 41425

Designed for 632.8nm

[17]:

n = 1.608
pitch = 0.25
length = 6.28
diameter = 2

gradient = pygrin.gradient(pitch, length)
print("expected gradient = 0.250,        calculated %.3f" % pitch)

efl = pygrin.EFL(n, pitch, length)
# print('expected EFL = 2.00,              calculated %.2f'%efl)

ffl = pygrin.FFL(n, pitch, length)
# print('expected FFL = -0.52,             calculated %.2f'%ffl)

bfl = pygrin.BFL(n, pitch, length)
# print('expected BFL = 4.52,              calculated %.2f'%bfl)

na = pygrin.NA(n, pitch, length, diameter)
print("expected NA = 0.38,               calculated %.2f" % na)

angle = pygrin.max_angle(n, pitch, length, diameter)
print("expected full accept angle = 45°, calculated %.0f°" % (2 * angle * 180 / np.pi))

print("working distance = %.2f mm" % (efl - ffl))

expected gradient = 0.250,        calculated 0.250
expected NA = 0.38,               calculated 0.38
expected full accept angle = 45°, calculated 45°
working distance = 2.49 mm

[18]:

pygrin.plot_principal_planes(n, pitch, length, diameter)
xpos = np.linspace(-diameter / 2, diameter / 2, 7)
for pos in xpos:
    z, r = pygrin.full_meridional_curve(n, pitch, length, ffl - efl, pos, pos)
    plt.plot(z, r, color="blue", lw=0.5)

plt.title("Oriel 41425")

plt.show()

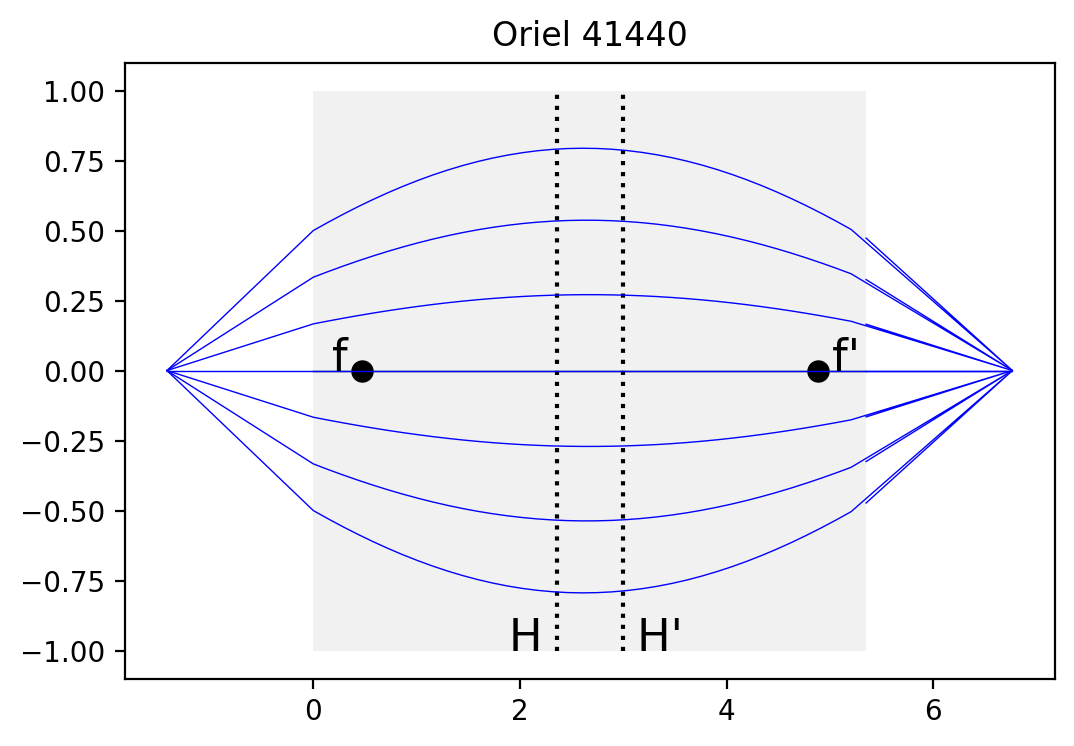
Oriel 41440

Designed for 632.8nm

[19]:

n = 1.608
pitch = 0.29
length = 5.35
diameter = 2

gradient = pygrin.gradient(pitch, length)
print("expected gradient = 0.290,        calculated %.3f" % pitch)

efl = pygrin.EFL(n, pitch, length)
# print('expected EFL = 2.00,              calculated %.2f'%efl)

ffl = pygrin.FFL(n, pitch, length)
# print('expected FFL = -0.52,             calculated %.2f'%ffl)

bfl = pygrin.BFL(n, pitch, length)
# print('expected BFL = 4.52,              calculated %.2f'%bfl)

na = pygrin.NA(n, pitch, length, diameter)
print("expected NA = 0.38,               calculated %.2f" % na)

angle = pygrin.max_angle(n, pitch, length, diameter)
print("expected full accept angle = 60°, calculated %.0f°" % (2 * angle * 180 / np.pi))

print("working distance = %.2f mm" % (efl - ffl))

expected gradient = 0.290,        calculated 0.290
expected NA = 0.38,               calculated 0.50
expected full accept angle = 60°, calculated 60°
working distance = 1.42 mm

[20]:

pygrin.plot_principal_planes(n, pitch, length, diameter)
xpos = np.linspace(-diameter / 4, diameter / 4, 7)
for pos in xpos:
    z, r = pygrin.full_meridional_curve(n, pitch, length, ffl - efl, 0, pos)
    plt.plot(z, r, color="blue", lw=0.5)

plt.title("Oriel 41440")
plt.show()

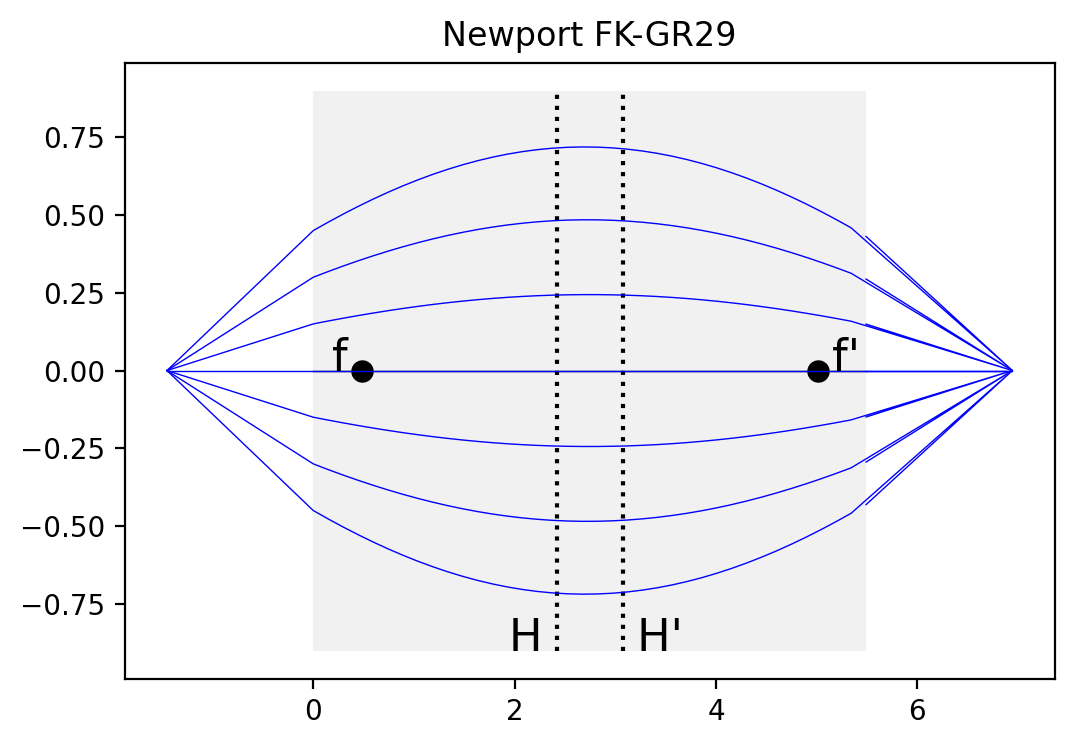
Newport FK - GR29

Designed for 850nm

[21]:

n = 1.608
pitch = 0.29
length = 5.49
diameter = 1.8

gradient = pygrin.gradient(pitch, length)
print("expected gradient = 0.290,        calculated %.3f" % pitch)

efl = pygrin.EFL(n, pitch, length)
print("expected EFL = 1.95,              calculated %.2f" % efl)

ffl = pygrin.FFL(n, pitch, length)
# print('expected FFL = -0.52,             calculated %.2f'%ffl)

bfl = pygrin.BFL(n, pitch, length)
# print('expected BFL = 4.52,              calculated %.2f'%bfl)

na = pygrin.NA(n, pitch, length, diameter)
print("expected NA = 0.46,               calculated %.2f" % na)

angle = pygrin.max_angle(n, pitch, length, diameter)
print("expected full accept angle = 60°, calculated %.0f°" % (2 * angle * 180 / np.pi))

print("working distance = %.2f mm" % (efl - ffl))

expected gradient = 0.290,        calculated 0.290
expected EFL = 1.95,              calculated 1.93
expected NA = 0.46,               calculated 0.45
expected full accept angle = 60°, calculated 53°
working distance = 1.45 mm

[22]:

pygrin.plot_principal_planes(n, pitch, length, diameter)
xpos = np.linspace(-diameter / 4, diameter / 4, 7)
for pos in xpos:
    z, r = pygrin.full_meridional_curve(n, pitch, length, ffl - efl, 0, pos)
    plt.plot(z, r, color="blue", lw=0.5)

plt.title("Newport FK-GR29")
plt.show()